실수 연산의 오류
Java에서 아래와 같은 code를 작성해 보자.
public static void main(String []args){
// #1. 0.3 - 0.1
System.out.println(0.3 - 0.1);
// #2. 0.1 1000번 더하기
double sum = 0;
for(int i=0; i<1000; i++){
sum += 0.1;
}
System.out.println(sum);
}
결과
0.19999999999999998
99.9999999999986
#1 code에서 0.3 - 0.1을 하였으나 0.2가 아닌 이상한 값이 출력된다.
#2 code 또한 0.1을 1000번 더하면 100이 되어야 하지만, 이상한 값이 출력되는 것을 볼 수 있다.
왜 이런 현상이 발생하는 걸까?
컴퓨터에서의 실수 표현
우리는 일상생활에서 10진수로 숫자를 표현하지만 컴퓨터는 숫자를 표현할 때 2진수를 사용한다.
10진수 실수를 2진수로 변환하는 방법은 아래와 같다.
10진수 실수 ↔ 2진수
10진수 소수부가 0으로 나누어 떨어질 때까지 2를 곱하며 1의 자리로 자리올림이 발생할 때마다 2진수를 채운다.
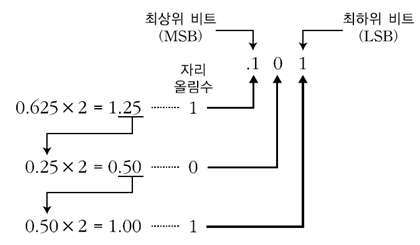
그림과 같이 0.625를 2진수로 변환하면 0.101⑵임을 알 수 있다.
이를 다시 10진수로 변환해보자.
- 0.101⑵
= 1*(1/2¹) + 0*(1/2²) + 1*(1/2³)
= 1*½ + 0*¼ + 1*⅛ = 0.5 + 0 + 0.125
= 0.625
0.625처럼 0으로 나누어 떨어지는 경우도 있지만 대부분의 경우 순환소수가 발생하게 된다.
위 code에서 다룬 0.1을 2진수로 변환해보자.
- 0.1 = 0.0001100110011...⑵
0.1의 경우 소수점 아래 숫자가 나누어 떨어지지 않고 계속 순환된다.
하지만, 컴퓨터에서는 무한정으로 숫자를 표현할 수 없다. (32bit 컴퓨터의 경우 32개 자릿수 이상의 2진수 표현 불가)
따라서 대부분의 실수의 경우 정확하게 표현이 불가능하며, 컴퓨터에는 가장 근사치의 값이 저장되는 것이다.
왜 0.3 - 0.1이 0.2가 아니라 0.19999999999999998로 출력되는지 알아보았다.
이번엔 컴퓨터에서 실수를 저장하는 방식에 알아보자.
고정 소수점 (Fixed point) 방식
고정 소수점 방식이란, 정수부와 소수부의 자릿수를 미리 정해놓고 실수를 표현하는 가장 간단한 방식이다.
예를 들어 32bit 시스템에서 고정소수점 방식으로 실수를 표현하기 위해 아래와 같이 정수부와 소수부를 구분해 보았다.
1bit 부호부는 숫자가 음수인지 양수인지 구분하는 MSB(Most Signficant bit)이다.
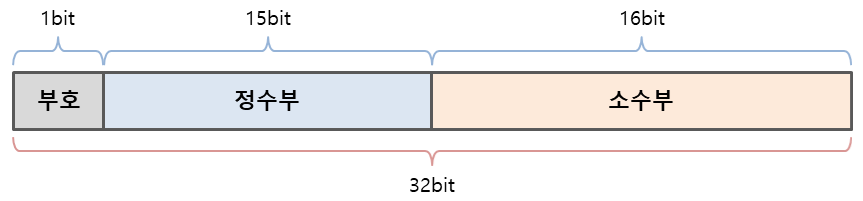
-14.1⑽를 위의 고정소수점 방식을 이용하여 2진수로 표현해보자.
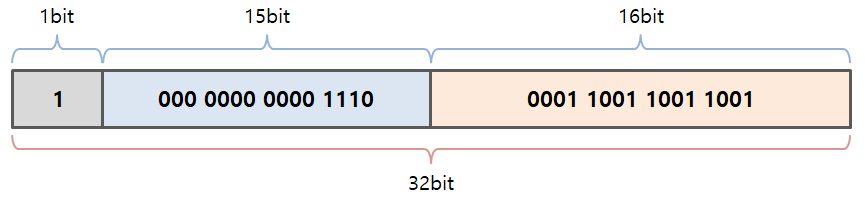
음수이기 때문에 부호 bit가 1이 되었으며, 14는 정수부에 0.1은 소수부에 각각 2진수로 변환하여 표현된다.
결과는 10000000 00001110 00011001 10011001⑵이다.
이처럼 고정소수점 방식을 사용하면 쉽고 간편하게 실수를 표현할 수 있다.
그러나 정수부와 소수부의 자릿수가 정해져 있어 표현할 수 있는 숫자의 범위가 매우 적다.
부동 소수점 (Floating point) 방식
고정소수점 방식에서는 실수를 정수부와 소수부로 나누어 표현하였다.
이로 인해 표현할 수 있는 숫자의 범위가 매우 적다는 단점이 발생하였다.
반면, 부동소수점 방식에서는 실수를 가수부와 지수부로 나누어 표현하여 이러한 단점을 해결하였다.
오늘날 일반적으로 대부분의 컴퓨터에서는 부동소수점 방식을 사용한다.
따라서 IEEE에서 정한 부동소수점 표현 방식을 표준 규약으로 정하여 이용한다.
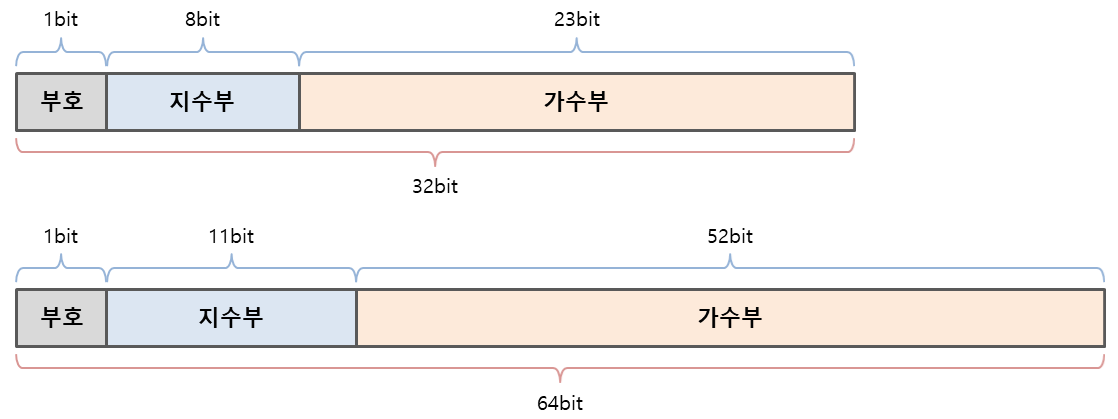
IEEE 754 표준에서는 32bit(float)와 64bit(double) 체계에서의 부동소수점 표현 방식을 정해놓았다.
우리는 좀 더 간편한 계산과 이해를 쉽게 돕기 위해 아래와 같은 8bit 체계의 환경을 준비하였다.
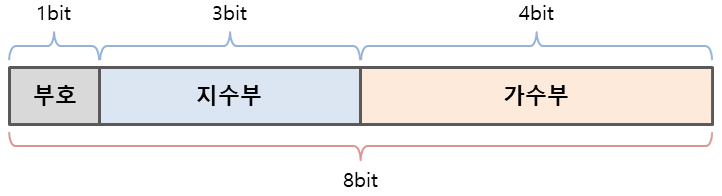
고정소수점에서 했던 것처럼 똑같이 -14.1⑽을 부동소수점 방식을 이용하여 표현해보자.
1. 2진수로 변환
(-) 1110.000110011...
2. Normalized form 적용
(-) 1.110000110011... * 2³
3. 부호, 지수부, 가수부 구하기
- 부호 : 1
- 지수부 : 3 = 101
- 가수부 : 110000110011...
4. 초과 표현 적용 (지수부)
음수 형태의 지수를 표현하기 위해 초과 표현(excess representation)을 사용한다.
초과표현 구하는 방법 : 2^(n-1) - 1 (n : 지수 bit)
우리는 지수부에 3bit를 할당했기 때문에 3 초과 표현을 사용한다. (2²-1)
따라서 지수부는 기존 3에 3을 초과시킨 6이 된다. (3+3)
(만약 지수부가 -2였다면, 3을 초과시켜 1이 되는 것이다.)
아래 표를 보면 이해가 좀 더 쉬울 것이다.
| 지수 (Decimal) |
3 초과표현 (Excess 3) |
2의 보수 (2's Complement) |
| -4 | 100 | |
| -3 | 000 | 101 |
| -2 | 001 | 110 |
| -1 | 010 | 111 |
| 0 | 011 | 000 |
| 1 | 100 | 001 |
| 2 | 101 | 010 |
| 3 | 110 | 011 |
| 4 | 111 |
5. 결과
따라서 부동소수점 방식에서 -14.1⑽를 표현한 결과는 아래와 같다.

