1. 이진탐색트리
1.1 이진탐색트리란?
이진탐색트리(BST: Binary Search Tree)는 이진트리 기반의 탐색을 위한 자료구조이다.
이진탐색의 효율적인 탐색 능력을 가지며, 삽입과 삭제가 가능한 것이 특징이다.
1.2 이진탐색트리의 4가지 조건
- 모든 노드는 유일한 키를 갖는다.
- 왼쪽 서브트리의 키들은 루트의 키보다 작다.
- 오른쪽 서브트리의 키들은 루트의 키보다 작다.
- 왼쪽과 오른쪽 서브트리도 이진탐색트리이다.
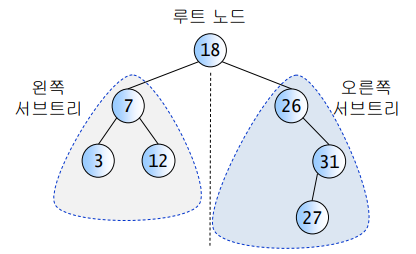
1.3 이진탐색트리 특징
이진탐색트리를 순회할 때는 중위순회(In-order Traversal) 방법을 사용한다.
(왼쪽 서브트리 → 루트 → 오른쪽 서브트리 순서)
이진탐색트리를 중위 순회한 결과는 트리 내의 모든 값들을 오름차순으로 정렬한 결과를 나타낸다.
예를 들어 위 그림의 트리를 중위 순회한 결과는 다음과 같다.
→ 3 7 12 18 26 27 31
1.4 이진탐색트리 ADT
객체
- 이진탐색트리의 4가지 조건을 만족하는 이진트리
연산
- search(key) : 키 값이 key인 노드를 찾아 반환
- insert(n) : 이진탐색트리의 특성을 유지하며 노드 n 삽입
- delete(n) : 이진탐색트리의 특성을 유지하며 노드 n 삭제
2. 이진탐색트리 연산
2.1 탐색
이진탐색트리에서 root 노드가 왼쪽 서브트리보다 크고 오른쪽 서브트리보다 작다는 점을 기억하자.
탐색 방법
- 찾고자하는 키와 현재 루트 노드의 키를 비교한다.
- 찾고자하는 키가 루트 노드의 키보다 작으면 왼쪽 자식 노드를 기준으로 다시 1번부터 시작한다.
찾고자하는 키가 루트 노드의 키보다 크면 오른쪽 자식 노드를 기준으로 다시 1번부터 시작한다. - 찾고자하는 키와 루트 노드의 키가 같으면 탐색이 종료된다.
굉장히 easy한 방법이다.
위의 알고리즘을 구현하려고 보니 순환(Recursive)을 써도 되고, 반복(Iterative)을 사용해도 된다.
각각의 방법을 이용하여 한번 구현해보자.
a. 순환으로 탐색 구현
// 탐색 (순환)
Node<T>* searchRecur(Node<T>* node, T key){
if(node == NULL) return NULL;
if(key == node->getData()) return node; // key == root 노드의 data
else if(key < node->getData()) return searchRecur(node->getLeft(), key); // key < root 노드의 data
else if(key > node->getData()) return searchRecur(node->getRight(), key); // key > root 노드의 data
}
b. 반복으로 탐색 구현
// 탐색 (반복)
Node<T>* searchIter(Node<T>* node, T key){
while(node != NULL){
if(key == node->getData()) return node; // key == root 노드의 data
else if(key < node->getData()) node = node->getLeft(); // key < root 노드의 data
else if(key > node->getData()) node = node->getRight(); // key > root 노드의 data
}
return NULL; // 탐색이 실패한 경우 NULL 반환
}
사실 효율성을 따지면 반복으로 구현한 탐색 함수가 훨씬 유리하다.
하지만 우리는 공부를 하는 단계이니 여러 방법으로 시도를 해봐야 도움이 될 것이다.
여기서 잠깐. 트리의 각 노드는 자신을 루트로 하는 이진트리가 될 수 있다.
그럼 Node 클래스에서 멤버 함수로 탐색을 구현해 보자.
c. Node 클래스에서 멤버함수로 순환 탐색 구현
template <typename T>
struct Node{
private:
T data;
Node* left;
Node* right;
public:
Node(T _data, Node* _left, Node* _right){
data = _data;
left = _left;
right = _right;
}
~Node(){}
// Node 멤버함수로 순환탐색 구현 (ㅎㅎ)
Node* search(T key){
if(key == data) // key == 노드의 data
return this;
else if(key < data && left != NULL) // key < 노드의 data
return left->search(key);
else if(key > data && right != NULL) // key > 노드의 data
return left->search(key);
else // 탐색이 실패한 경우
return NULL;
}
...
}여러가지 방법으로 탐색 알고리즘을 구현해 보았다.
여기서 알 수 있듯이 이진탐색트리 탐색 연산의 시간복잡도는 트리의 높이가 h 일 때 O(h)가 된다.
2.2 삽입
이진탐색트리에 삽입을 하기 위해서는 이진탐색트리의 조건을 만족하는 위치를 찾아 새로운 노드를 추가해야 한다.
삽입 방법
- 추가하고자 하는 key로 탐색을 수행한다.
- 이진탐색트리에는 중복된 key가 있을 수 없으므로, 추가하고자 하는 key를 갖는 노드가 있다면 삽입이 불가능하다.
- 탐색에 실패한다면 실패한 위치가 바로 새로운 노드가 삽입 되는 위치가 된다.
왜 3번에서 탐색이 실패한 위치에 새로운 노드가 삽입되는 지는 탐색을 이해하였다면 충분히 이해했으리라고 생각한다.
순환을 이용하여 삽입 구현
// 삽입 (순환)
void insertRecur(Node<T>* node, T key){
Node<T>* newNode = new Node<T>(key, nullptr, nullptr); // 새로운 key를 가지는 node 생성
if(key == node->getData()){ // 트리에 이미 key값을 가지는 node가 있는 경우
return;
}else if(key < node->getData()){ // key < root 노드의 data
if(node->getLeft() == NULL){
node->setLeft(newNode);
}else{
insertRecur(node->getLeft(), key);
}
}else if(key > node->getData()){ // key > root 노드의 data
if(node->getRight() == NULL){
node->setRight(newNode);
}else{
insertRecur(node->getRight(), key);
}
}
}
이진탐색트리 삽입 연산의 시간복잡도 또한 탐색 연산과 동일하게 트리의 높이가 h 일 때 O(h)가 된다.
물론 삽입이라는 계산이 한번 추가되지만, O(1) 수준이므로 무시한다.
2.3 삭제
이진탐색트리에서 삭제는 기존 노드를 삭제하면서 이진탐색트리의 조건을 만족시켜야 하므로, 탐색과 삽입 연산보다 조금 복잡하다.
삭제 시 발생할 수 있는 경우의 수는 3가지이다.
- 삭제하려는 노드가 leaf 노드인 경우
- 삭제하려는 노드가 왼쪽이나 오른쪽 자식노드 중 하나만 가지고 있는 경우
- 삭제하려는 노드가 두 개의 자식노드를 모두 가지고 있는 경우
첫 번째 "삭제하려는 노드가 leaf 노드인 경우" 해당 노드만 삭제하면 된다.
즉 부모노드를 찾아서 부모노드에서 해당 link를 null로 만들어 연결을 끊으면 되고, 동적으로 할당된 노드였을 경우 메모리 반납까지 해주면 된다.
두 번째 "삭제하려는 노드가 하나의 자식노드만 가지는 경우" 해당 노드의 부모노드와 자식노드를 연결해주면 된다.
LinkedList에서의 삭제를 생각하면 이해가 쉬울 것이다.
부모노드를 찾아서 부모노드에서 해당 link를 자식노드의 link로 연결시켜주면 된다.
역시나 마찬가지로 동적으로 할당된 노드였을 경우 삭제 노드를 먼저 반납해야 한다.
마지막으로 "삭제하려는 노드가 두개의 자식노드를 모두 가지는 경우" 조금 복잡하다.
그림을 보며천천히 생각해 보자.
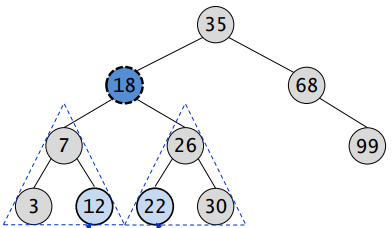
18 노드를 삭제한다고 가정했을 때 노드가 삭제된 후 그 자리를 누가 채워야 할까?
그림에서 유추했듯이 정답은 왼쪽 서브트리에서 가장 큰 값 또는 오른쪽 서브트리에서 가장 작은 값이다.
이유는 단순하다.
그래야만 이진탐색트리의 조건을 만족하며 트리의 변동성을 최소화할 수 있기 때문이다.
이진탐색트리를 중위 순회하면, 우리가 알다시피 Left → Root → Right 순서로 순회한다.
Left는 왼쪽 서브트리에서 가장 오른쪽 아래의 node이며, Right는 오른쪽 서브트리에서 가장 왼쪽 아래의 node이다.
따라서 위 트리에서 삭제될 18 노드의 이전 노드는 12 노드이며, 이후 노드는 22 노드이다.
이들 중 하나를 삭제될 노드 자리에 채우면 삭제 이후 이진탐색트리의 형태가 유지되는 것이다.
삭제 구현
// 삭제
void remove(Node<T>* parentNode, Node<T>* deleteNode){
// Case1. 삭제하려는 node가 leaf 노드인 경우
if(deleteNode->isLeaf()){
if(deleteNode == this->getRoot()){ // 삭제하려는 node가 root인 경우
this->setRoot(nullptr);
}else{
if(parentNode->getLeft() == deleteNode){ // parent의 왼쪽 자식노드 삭제
parentNode->setLeft(nullptr);
}else if(parentNode->getRight() == deleteNode){ // parent의 오른쪽 자식노드 삭제
parentNode->setRight(nullptr);
}
}
}
// Case2. 삭제하려는 node가 하나의 자식노드만 갖는 경우
else if(deleteNode->getLeft() == NULL || deleteNode->getRight() == NULL){
Node<T>* childNode = (deleteNode->getLeft() != NULL) ? deleteNode->getLeft() : deleteNode->getRight(); // 삭제할 node의 유일한 자식노드
if(deleteNode == this->getRoot()){ // 삭제하려는 node가 root인 경우
this->setRoot(childNode);
}else{
if(parentNode->getLeft() == deleteNode){ // parent의 왼쪽 자식노드에 childNode link
parentNode->setLeft(childNode);
}else if(parentNode->getRight() == deleteNode){ // parent의 오른쪽 자식노드 childNode link
parentNode->setRight(childNode);
}
}
}
// Case3. 삭제하려는 node가 2개의 자식노드를 모두 갖는 경우
else{
// 삭제하려는 노드의 오른쪽 서브트리에서 가장 작은 노드를 탐색하는 과정
Node<T>* succp = deleteNode;
Node<T>* succ = deleteNode->getRight();
while(succ->getLeft() != NULL){
succp = succ;
succ = succ->getLeft();
}
// 3-1. 후계자 노드의 부모와 후계자 노드의 자식 연결
if(succp->getLeft() == succ){
succp->setLeft(succ->getRight());
}else{ // 후계자 노드가 삭제할 노드의 바로 오른쪽 자식인 경우
succp->setRight(succ->getRight());
}
// 3-2. 삭제할 노드의 data를 후계자노드의 data로 대체
deleteNode->setData(succ->getData());
// 3-3. 삭제할 노드를 후계자노드로 변경 (후계자노드를 delete 하기 위해)
deleteNode = succ;
}
delete deleteNode; // memory 반납
}
트리의 높이가 h 이고 삭제 대상 노드의 레벨이 d 일 때 h-d 만큼의 비교 연산을 수행해야 한다.
복사 및 삭제 과정의 연산은 상수시간으로 무시하면, 이진탐색트리 삭제연산의 시간복잡도 또한 O(h)이다.
2.4 이진탐색트리 연산의 시간복잡도
위에서 알아본 것과 같이 이진탐색트리의 탐색, 삽입, 삭제 연산의 시간복잡도는 모두 O(h)이다.
h는 트리의 높이이며, 이전 글에서 아래와 같이 공부했었다.
❝ n개의 노드를 가지는 이진트리에서 최소 높이는 $h ≥ \lceil{log_2(n+1)}\rceil$ 이며, 최대 높이는 n이다. ❞
결과적으로 최악의 경우 (경사이진트리 모양) 이진탐색트리의 시간복잡도는 O(n)이다.
하지만 최선의 경우 (포화이진트리 모양) 이진탐색트리의 시간복잡도는 O(log₂n)이 된다.
2.5 C++ 이진탐색트리 구현 (전체 소스코드)
#include <iostream>
#include <queue>
using namespace std;
template <typename T>
struct Node{
private:
T data;
Node* left;
Node* right;
public:
Node(T _data, Node* _left, Node* _right){
data = _data;
left = _left;
right = _right;
}
~Node(){}
// getter/setter
T getData(){
return data;
}
void setData(T _data){
data = _data;
}
Node* getLeft(){
return left;
}
void setLeft(Node* _left){
left = _left;
}
Node* getRight(){
return right;
}
void setRight(Node* _right){
right = _right;
}
// is leaf node?
bool isLeaf(){
return left==nullptr && right==nullptr;
}
// Node 멤버함수로 순환탐색 구현 (ㅎㅎ)
Node* search(T key){
if(key == data) // key == 노드의 data
return this;
else if(key < data && left != NULL) // key < 노드의 data
return left->search(key);
else if(key > data && right != NULL) // key > 노드의 data
return left->search(key);
else // 탐색이 실패한 경우
return NULL;
}
};
template <typename T>
class BinaryTree{
private:
Node<T>* root;
public:
BinaryTree(){
root = nullptr;
}
~BinaryTree(){}
// set root node
void setRoot(Node<T>* _root){
root = _root;
}
// get root node
Node<T>* getRoot(){
return root;
}
// 전위 순회(Pre-order Traversal)
void preorder(){
cout << "Preorder : [ ";
preorder(root);
cout << "]" << endl;
}
void preorder(Node<T>* node){
if(node != NULL){
cout << node->getData() << " ";
preorder(node->getLeft());
preorder(node->getRight());
}
}
// 중위 순회(In-order Traversal)
void inorder(){
cout << "Inorder : [ ";
inorder(root);
cout << "]" << endl;
}
void inorder(Node<T>* node){
if(node != NULL){
inorder(node->getLeft());
cout << node->getData() << " ";
inorder(node->getRight());
}
}
// 후위 순회(Post-order Traversal)
void postorder(){
cout << "Postorder : [ ";
postorder(root);
cout << "]" << endl;
}
void postorder(Node<T>* node){
if(node != NULL){
postorder(node->getLeft());
postorder(node->getRight());
cout << node->getData() << " ";
}
}
// 레벨 순회(Level-order Traversal)
void levelorder(){
cout << "Levelorder: [ ";
if(!isEmpty()){
queue<Node<T>*> q;
q.push(root);
while(!q.empty()){
Node<T>* node = q.front();
q.pop();
if(node != NULL){
cout << node->getData() << " ";
q.push(node->getLeft());
q.push(node->getRight());
}
}
}
cout << "]" << endl;
}
// 전체 노드 개수 구하기
int getCount(){
return isEmpty() ? 0 : getCount(root);
}
int getCount(Node<T>* node){
if(node == NULL) return 0;
return 1 + getCount(node->getLeft()) + getCount(node->getRight());
}
// leaf 노드 개수 구하기
int getLeafCount(){
return isEmpty() ? 0 : getLeafCount(root);
}
int getLeafCount(Node<T>* node){
if(node == NULL) return 0;
if(node->isLeaf()) return 1;
else return getLeafCount(node->getLeft()) + getLeafCount(node->getRight());
}
// 트리 높이 구하기
int getHeight(){
return isEmpty() ? 0 : getHeight(root);
}
int getHeight(Node<T>* node){
if(node == NULL) return 0;
int lHeight = getHeight(node->getLeft()); // 왼쪽 서브트리 높이 계산
int rHeight = getHeight(node->getRight()); // 오른쪽 서브트리 높이 계산
return (lHeight > rHeight) ? lHeight + 1 : rHeight + 1;
}
bool isEmpty(){
return root == nullptr;
}
};
// 이진탐색트리 (이진트리 상속)
template <typename T>
class BinarySearchTree : public BinaryTree<T>{
private:
// 탐색 (순환)
Node<T>* searchRecur(Node<T>* node, T key){
if(node == NULL) return NULL;
if(key == node->getData()) return node; // key == root 노드의 data
else if(key < node->getData()) return searchRecur(node->getLeft(), key); // key < root 노드의 data
else if(key > node->getData()) return searchRecur(node->getRight(), key); // key > root 노드의 data
}
// 탐색 (반복)
Node<T>* searchIter(Node<T>* node, T key){
while(node != NULL){
if(key == node->getData()) return node; // key == root 노드의 data
else if(key < node->getData()) node = node->getLeft(); // key < root 노드의 data
else if(key > node->getData()) node = node->getRight(); // key > root 노드의 data
}
return NULL; // 탐색이 실패한 경우 NULL 반환
}
// 삽입 (순환)
void insertRecur(Node<T>* node, T key){
Node<T>* newNode = new Node<T>(key, nullptr, nullptr); // 새로운 key를 가지는 node 생성
if(key == node->getData()){ // 트리에 이미 key값을 가지는 node가 있는 경우
return;
}else if(key < node->getData()){ // key < root 노드의 data
if(node->getLeft() == NULL){
node->setLeft(newNode);
}else{
insertRecur(node->getLeft(), key);
}
}else if(key > node->getData()){ // key > root 노드의 data
if(node->getRight() == NULL){
node->setRight(newNode);
}else{
insertRecur(node->getRight(), key);
}
}
}
// 삭제
void remove(Node<T>* parentNode, Node<T>* deleteNode){
// Case1. 삭제하려는 node가 leaf 노드인 경우
if(deleteNode->isLeaf()){
if(deleteNode == this->getRoot()){ // 삭제하려는 node가 root인 경우
this->setRoot(nullptr);
}else{
if(parentNode->getLeft() == deleteNode){ // parent의 왼쪽 자식노드 삭제
parentNode->setLeft(nullptr);
}else if(parentNode->getRight() == deleteNode){ // parent의 오른쪽 자식노드 삭제
parentNode->setRight(nullptr);
}
}
}
// Case2. 삭제하려는 node가 하나의 자식노드만 갖는 경우
else if(deleteNode->getLeft() == NULL || deleteNode->getRight() == NULL){
Node<T>* childNode = (deleteNode->getLeft() != NULL) ? deleteNode->getLeft() : deleteNode->getRight(); // 삭제할 node의 유일한 자식노드
if(deleteNode == this->getRoot()){ // 삭제하려는 node가 root인 경우
this->setRoot(childNode);
}else{
if(parentNode->getLeft() == deleteNode){ // parent의 왼쪽 자식노드에 childNode link
parentNode->setLeft(childNode);
}else if(parentNode->getRight() == deleteNode){ // parent의 오른쪽 자식노드 childNode link
parentNode->setRight(childNode);
}
}
}
// Case3. 삭제하려는 node가 2개의 자식노드를 모두 갖는 경우
else{
// 삭제하려는 노드의 오른쪽 서브트리에서 가장 작은 노드를 탐색하는 과정
Node<T>* succp = deleteNode;
Node<T>* succ = deleteNode->getRight();
while(succ->getLeft() != NULL){
succp = succ;
succ = succ->getLeft();
}
// 3-1. 후계자 노드의 부모와 후계자 노드의 자식 연결
if(succp->getLeft() == succ){
succp->setLeft(succ->getRight());
}else{ // 후계자 노드가 삭제할 노드의 바로 오른쪽 자식인 경우
succp->setRight(succ->getRight());
}
// 3-2. 삭제할 노드의 data를 후계자노드의 data로 대체
deleteNode->setData(succ->getData());
// 3-3. 삭제할 노드를 후계자노드로 변경 (후계자노드를 delete 하기 위해)
deleteNode = succ;
}
delete deleteNode; // memory 반납
}
public:
BinarySearchTree(){}
~BinarySearchTree(){}
// 탐색
Node<T>* search(T key){
//return searchRecur(this->getRoot(), key);
return searchIter(this->getRoot(), key);
}
// 삽입
void insert(T key){
if(this->isEmpty()){
Node<T>* newNode = new Node<T>(key, nullptr, nullptr); // 새로운 key를 가지는 node 생성
this->setRoot(newNode);
}else{
insertRecur(this->getRoot(), key);
}
}
// 삭제
void remove(T key){
if(this->isEmpty()){
cout << "Tree is Empty" << endl;
return;
}
// parentNode와 deleteNode를 찾는 과정
Node<T>* parentNode = nullptr; // 삭제하려는 node의 부모 node (최초 root의 부모노드는 없음)
Node<T>* deleteNode = this->getRoot(); // 삭제하려는 node
while(deleteNode != NULL && deleteNode->getData() != key){
parentNode = deleteNode;
deleteNode = (key < parentNode->getData()) ? parentNode->getLeft() : parentNode->getRight();
}
if(deleteNode == NULL){
cout << "Key is not in Tree" << endl;
return;
}else{
remove(parentNode, deleteNode);
}
}
};int main(){
BinarySearchTree<int> tree;
// 10개 node 삽입
tree.insert(35);
tree.insert(18);
tree.insert(7);
tree.insert(26);
tree.insert(12);
tree.insert(3);
tree.insert(68);
tree.insert(22);
tree.insert(30);
tree.insert(99);
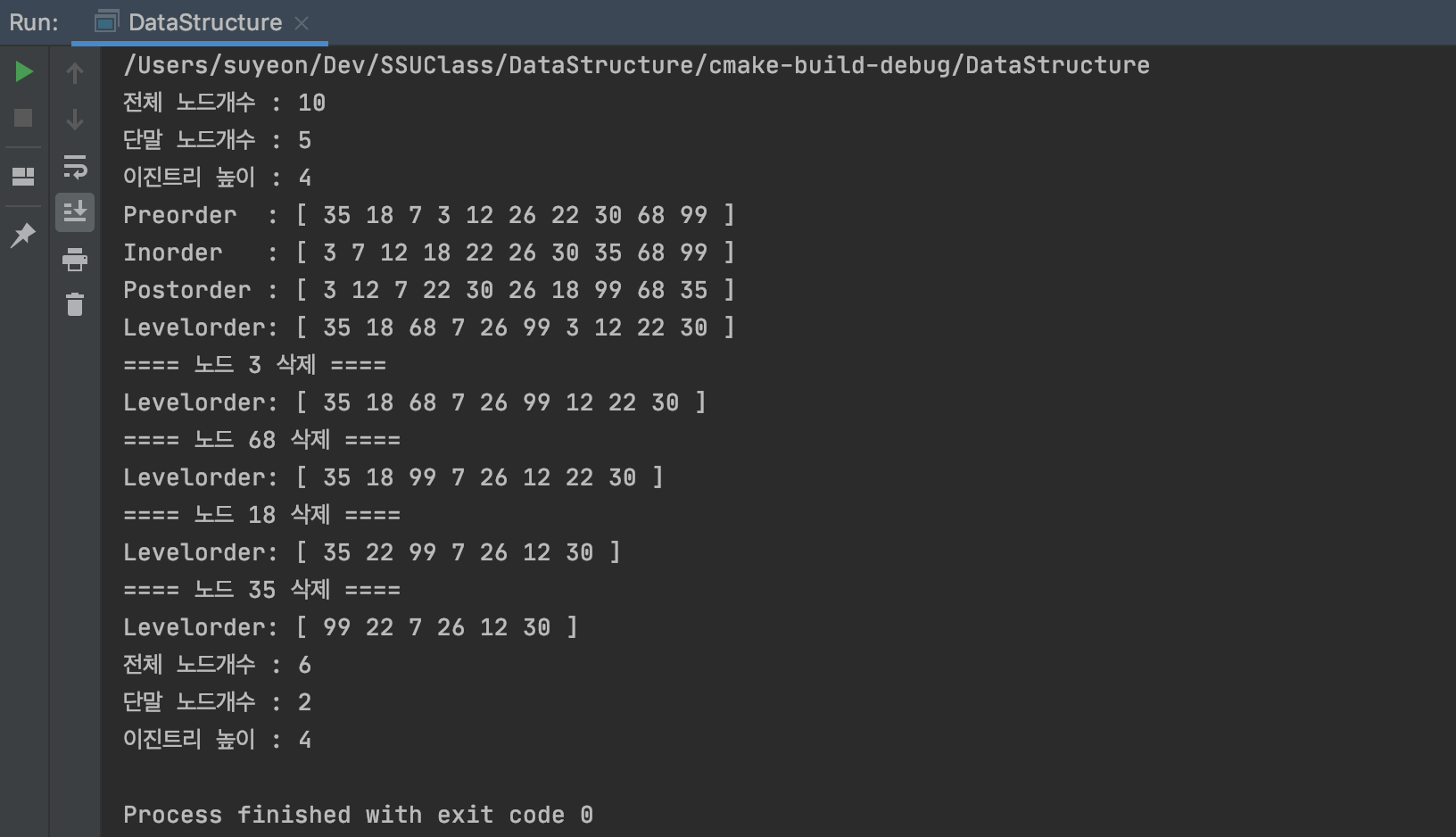
// Calculate
cout << "전체 노드개수 : " << tree.getCount() << endl;
cout << "단말 노드개수 : " << tree.getLeafCount() << endl;
cout << "이진트리 높이 : " << tree.getHeight() << endl;
// Traversal
tree.preorder();
tree.inorder();
tree.postorder();
tree.levelorder();
// 삭제
cout << "==== 노드 3 삭제 ====" << endl;
tree.remove(3);
tree.levelorder();
cout << "==== 노드 68 삭제 ====" << endl;
tree.remove(68);
tree.levelorder();
cout << "==== 노드 18 삭제 ====" << endl;
tree.remove(18);
tree.levelorder();
cout << "==== 노드 35 삭제 ====" << endl;
tree.remove(35);
tree.levelorder();
// Last Calculate
cout << "전체 노드개수 : " << tree.getCount() << endl;
cout << "단말 노드개수 : " << tree.getLeafCount() << endl;
cout << "이진트리 높이 : " << tree.getHeight() << endl;
return 0;
}
![[자료구조] 이진탐색트리 (Binary Search Tree)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FQFfvN%2FbtqSjB2nU4o%2FmNjK5Oj7WpYkxfkdlBZXk0%2Fimg.png)