![[자료구조] 순환 (Recursion) - 팩토리얼, 거듭제곱 계산, 피보나치 수열, 하노이의 탑, 영역 채색](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FrdDeN%2FbtqSa80t5Vx%2FDMncHZY9hYmEQO1bEVOJ0K%2Fimg.png)
1. 순환
1.1 순환이란?
순환(Recursion)은 컴퓨터 과학에서 재귀라고도 하며 자신을 정의할 때 자기 자신을 재참조하는 방법을 뜻한다.
순환은 알고리즘을 해결하는데 사용되는 일종의 프로그래밍 기법이며, 트리 자료구조를 공부하기에 앞서 간단하게 알아보자.
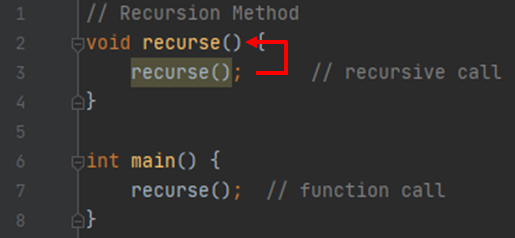
1.2 반복 vs 순환
프로그래밍 언어에서 같은 일을 반복하기 위한 방법에는 반복(iteration)과 순환(recursion)이 있다.
반복이란 for나 while 등의 반복문을 사용하여 조건이 만족할 때까지 계속하여 반복시키는 방식이다.
순환은 위에서 말한대로 method가 자기 자신을 다시 호출하는 방식을 의미한다.
일반적으로 순환은 method 호출을 하게 되므로 반복에 비해 수행 속도가 떨어진다.
하지만, 필요한 경우 순환을 사용하면 반복을 사용하는 것보다 훨씬 간단하고 효율적으로 문제를 해결할 수 있다.
각각의 경우에 따라 상황에 맞게 반복과 순환 중 선택을 하면 된다.
2. 팩토리얼
2.1 팩토리얼의 정의
n! = n · (n-1) · (n-2) · (n-3) · ··· · 3 · 2 · 1
팩토리얼(Factorial)은 1에서부터 n까지의 범위에 있는 모든 정수를 곱하는 것을 의미한다.
예를들어 5! = 5 · 4 · 3 · 2 · 1 = 120이다.
양의 정수 n의 팩토리얼은 아래와 같이 정의할 수 있다.
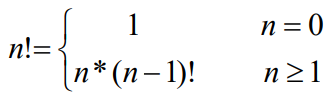
위의 정의에서 n!을 정의하는데 다시 (n-1)!가 사용되었다.
이러한 구조가 순환 구조인 것이다.
이를 코드로 작성해보자.
2.2 팩토리얼 구현 (순환) C++
int factorial(int n){
if(n==1) return 1;
else return (n * factorial(n-1));
}line3에서 위의 공식처럼 다시 자기 자신(factorial)을 호출하는 것을 볼 수 있다.
3!을 구하는 경우 factorial(3)은 아래와 같이 동작된다.
또한 순환 알고리즘에서는 반드시 순환 호출을 멈추는 조건이 필요하다.
팩토리얼 코드에서는 line2에서 n=1 일 때 순환을 멈추고 상수 1을 반환한다.
만약 순환호출을 멈추는 조건이 없다면, 시스템 오류가 발생할 때까지 자기자신을 무한히 호출하며 무한루프에 빠지게 될 것이다.
3. 거듭제곱 계산
xⁿ을 구하기 위해서는 일반적으로 x를 n번 반복적으로 더하는 방법을 사용한다.
하지만 순환을 이용해서 거듭제곱 계산을 할 수 도 있다.
xⁿ을 구하는 코드를 반복과 순환호출 방법으로 각각 구현하고 비교해보자.
3.1 거듭제곱 계산 구현 (반복)
double power(double x, int n){
double r = 1.0;
for(int i=0; i<n; i++){
r = r*x;
}
return r;
}n만큼 반복하며 x를 곱해가는 방식이다.
당연히 시간복잡도는 O(n)이다.
3.2 거듭제곱 계산 구현 (순환호출)
double power(double x, int n){
if(n==0) return 1.0;
else if ((n%2)==0) // n이 짝수인 경우
return power(x*x, n/2);
else // n이 홀수인 경우
return x * power(x*x, (n-1)/2);
}n이 짝수인 경우 x²을 먼저 계산한 후 이 값을 n/2로 제곱한다.
n이 홀수인 경우 x²을 먼저 계산한 후 이 값을 (n-1)/2로 제곱하고 x를 한 번 더 곱해준다.
2¹⁰을 계산하는 경우 아래와 같이 동작한다.
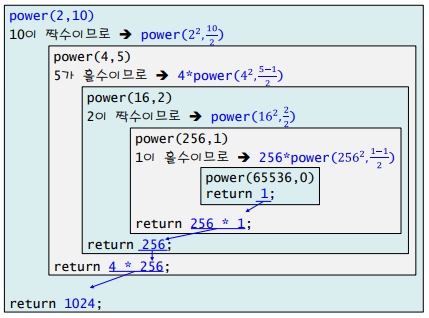
한번 순환할 때마다 반복 횟수가 절반씩(n/2) 줄어드는 것을 알 수 있다.
이를 시간복잡도로 나타내면 O(log₂n)이다.
3.3 정리
반복을 사용하여 거듭제곱을 계산하는 것보다, 순환호출을 사용하여 거듭제곱을 계산하는 경우 시간복잡도 측면에서 더욱 효율적임을 알 수 있다.
- 반복
O(n)> 순환호출O(log₂n)
4. 피보나치 수열 계산
4.1 피보나치 수열 정의
수학에서 피보나치 수(Fibonacci numbers)는 첫째 및 둘째 항이 1이며 그 뒤의 모든 항은 바로 앞 두 항의 합인 수열이다.
편의상 0번째 항을 0으로 두기도 한다.
피보나치 수 ${\displaystyle F_{n}}$을 정의하면 다음과 같다.
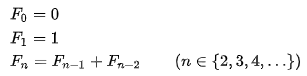
위 점화식을 보아하니 피보나치 수열 또한 순환호출을 이용하여 구현이 가능한 것을 알 수 있다.
이번에는 피보나치 수열을 구하는 코드를 반복과 순환호출 방법으로 각각 구현하고 비교해보자.
4.2 피보나치 수열 계산 구현 (반복)
int fibo(int n){
if(n<2) return n;
else{
int tmp, current=1, last=0;
for(int i=2; i<=n; i++){
tmp = current;
current += last;
last = tmp;
}
return current;
}
}2~n만큼 반복하며 순차적으로 두 항의 수를 더해나가는 방법이다.
당연히 시간복잡도는 O(n)이다.
4.3 피보나치 수열 계산 구현 (순환호출)
int fibo(int n){
if(n==0) return 0;
if(n==1) return 1;
else return (fibo(n-1) + fibo(n-2));
}반복문을 이용하여 구현한 코드에 비해 단순하고 이해하기 쉽게 구현되었다.
하지만 실제로는 매우 비효율적이다.
예를들어 fibo(6)을 계산하는 경우 아래와 같이 동작한다.
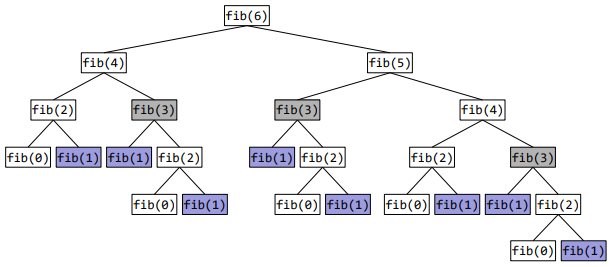
fibo(6)를 호출하면 fibo(4)가 2번 호출된다. fibo(3)은 3번 호출되며 fibo(2)는 5번 호출된다.
fibo(6)을 구하기 위해 fibo() 함수가 총 25번이나 호출되었다.
순환 단계가 깊어질수록 이러한 현상은 더욱 심해진다.
이를 시간복잡도로 나타내면 O(2ⁿ)이다.
4.4 정리
피보나치 수열을 계산하는 경우 순환호출을 사용하는 것보다 반복으로 문제를 해결하는 것이 훨씬 효율적이다.
- 반복
O(n)< 순환호출O(2ⁿ)
이렇듯 문제에 따라 반복 또는 순환호출 중 적절한 방법을 선택하여 사용해야 한다.
5. 하노이 탑
5.1 하노이 탑이란?
하노이의 탑(Tower of Hanoi)은 퍼즐의 일종이다. 세 개의 기둥과 이 기둥에 꽂을 수 있는 크기가 다양한 원판들이 있고, 퍼즐을 시작하기 전에는 한 기둥에 원판들이 작은 것이 위에 있도록 순서대로 쌓여 있다.
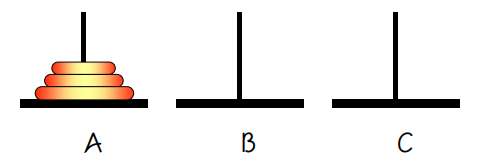
게임의 목적은 다음 조건을 만족시키면서, 한 기둥에 꽂힌 원판들을 그 순서 그대로 다른 기둥으로 옮겨서 다시 쌓는 것이다.
|
1. 한 번에 하나의 원판만 이동할 수 있다. |
하노이의 탑 이동순서
5.2 하노이의 탑 구현
#include <iostream>
using namespace std;
void hanoi(int n, char from, char tmp, char to){
if(n==1){
cout << n << ": " << from << " -> " << to << endl;
}else{
hanoi(n-1, from, to, tmp); // A의 맨 밑을 제외한 나머지 원판들을 B로 옮김
cout << n << ": " << from << " -> " << to << endl; // A에 남은 한 개의 원판(맨 밑)을 C로 옮김
hanoi(n-1, tmp, from, to); // B의 원판들을 C로 옮김
}
}
int main(){
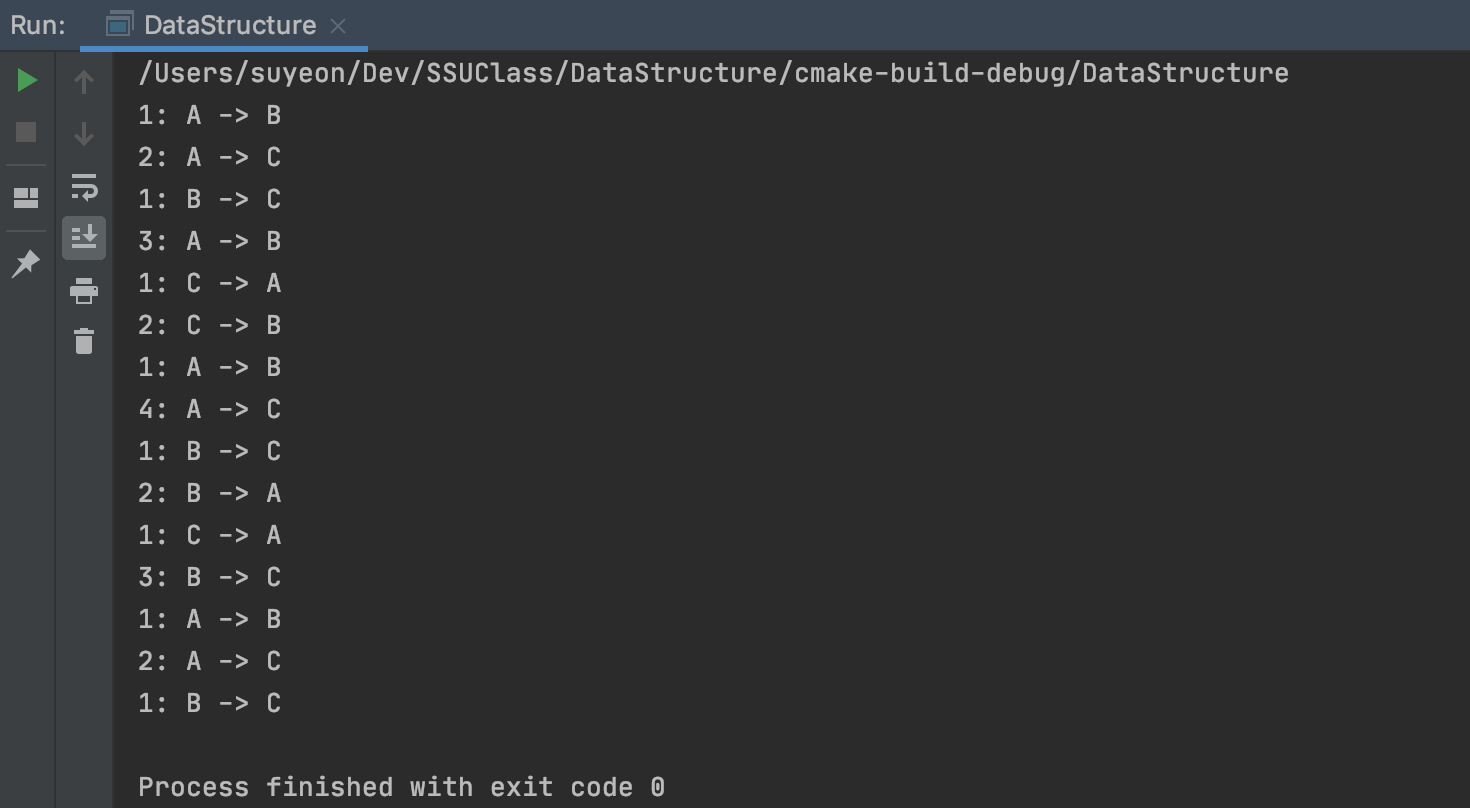
hanoi(4, 'A', 'B', 'C');
return 0;
}
6. 영역채색
6.1 영역채색이란?
영상처리 분야에서 영역 채색(Blob coloring) 또는 연결화소 분석법(Connected Component Labeling)이라 불리는 알고리즘은 BW 이미지에서 연결된 객체를 찾는 방법이다.
6.2 영역채색 구현
#include <iostream>
#include <vector>
using namespace std;
#define WIDTH 20
#define HEIGHT 9
// 근접 4방향 화소가 이어져있는지 판단하여 labeling
void labelComponent(unsigned int img[HEIGHT][WIDTH], int x, int y, int label){
if(x<0 || y<0 || x>=WIDTH || y>=HEIGHT){ // 이미지 영역 밖인 경우 return
return;
}
if (img[y][x] == 9){ // labeling 처리가 안된 black 픽셀인 경우
img[y][x] = label; // 해당 픽셀에 label값 부여
// (4방향 연결) 좌,상,우,하 방향으로 순환호출
labelComponent(img, x-1, y, label);
labelComponent(img, x, y-1, label);
labelComponent(img, x+1, y, label);
labelComponent(img, x, y+1, label);
}
}
// BW 이미지 영역채색
void blobColoring(unsigned int img[HEIGHT][WIDTH]){
int label = 1; // label 초기화
// [0,0] 화소부터 모든 화소에 대해 차례대로 loop 돌면서 labeling 처리가 안된 화소인 경우 labelComponent() 호출
for(int y=0; y<HEIGHT; y++){
for(int x=0; x<WIDTH; x++){
if(img[y][x] == 9){
labelComponent(img, x, y, label++);
}
}
}
}
// 이미지 출력
void printImage(unsigned int img[HEIGHT][WIDTH]){
for(int y=0; y<HEIGHT; y++){
for(int x=0; x<WIDTH; x++){
if(img[y][x] == 0){
cout << ".";
}else{
cout << img[y][x];
}
}
cout << endl;
}
cout << endl;
}
int main(){
unsigned int image[HEIGHT][WIDTH] = {0,0,0,0,0,0,9,0,0,0,0,9,9,9,9,9,0,0,9,9,
9,9,9,9,9,0,9,0,0,0,0,0,0,0,0,9,0,0,9,9,
0,0,9,0,0,0,9,0,0,0,0,9,9,9,9,9,0,0,9,9,
0,9,9,9,0,0,9,9,9,0,0,9,0,0,0,0,0,0,9,9,
0,9,0,9,0,0,9,0,0,0,0,9,9,9,9,9,0,0,9,9,
9,9,0,9,9,0,9,0,0,0,0,0,0,0,0,0,0,0,9,9,
9,0,0,0,9,0,9,0,0,0,0,0,9,0,9,0,0,0,0,0,
9,0,0,0,9,0,9,0,0,0,0,0,9,0,9,0,0,0,9,9,
0,0,0,0,0,0,9,0,0,0,0,9,9,9,9,9,0,0,9,9};
cout << "<Original Image>" << endl;
printImage(image);
cout << "<Labelled Image>" << endl;
blobColoring(image);
printImage(image);
return 0;
}
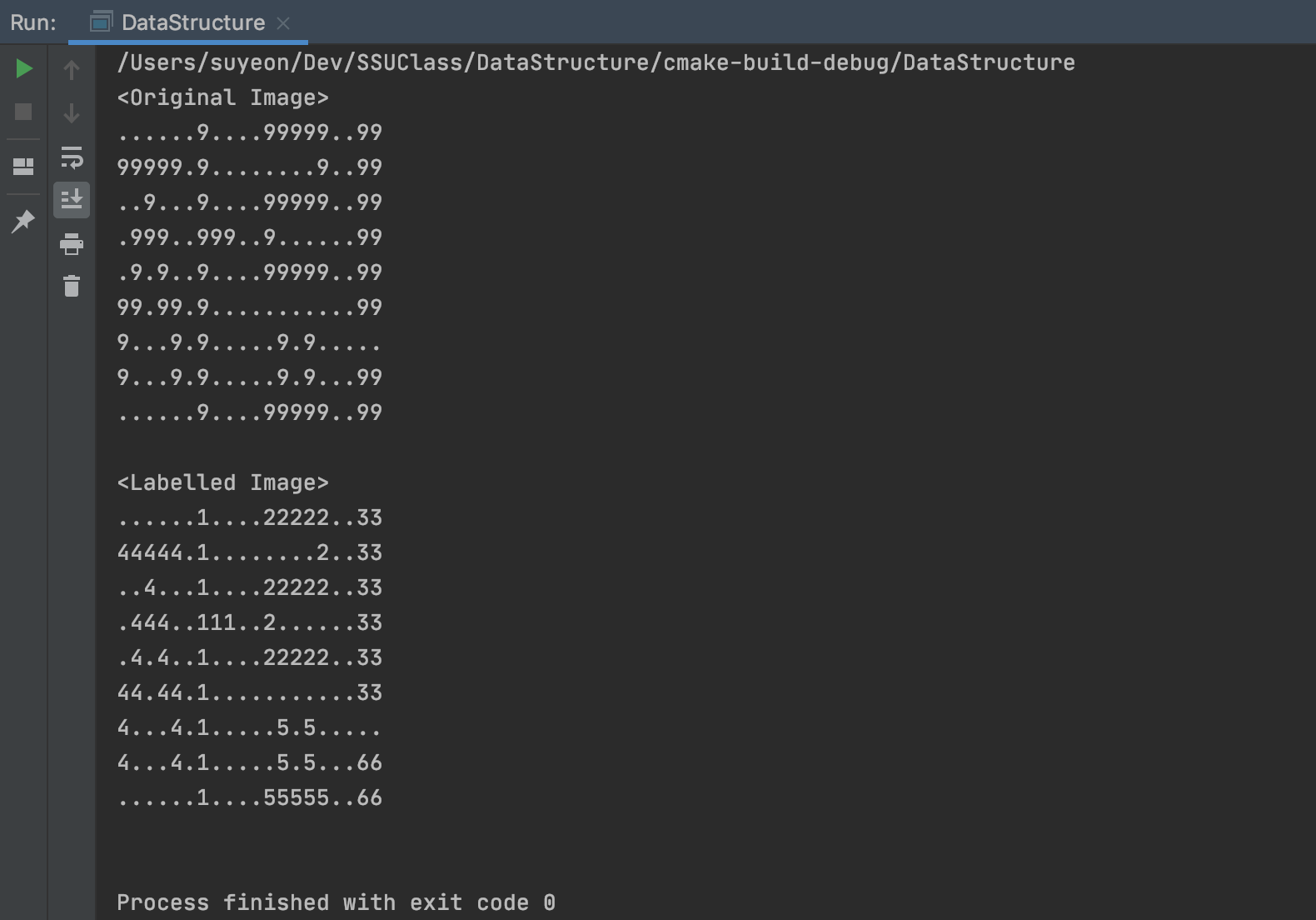
이미지의 [0,0] 위치에서부터 차례대로 loop를 돌며 labeling 되지않은 검은색 pixel(9)을 마주치면 labelComponent(x, y)를 호출한다.
labelComponent(x, y)에서는 (x, y) 픽셀이 labeling 되지않은 검은색 pixel(9)이면 label값을 부여하고 인접한 4방향의 픽셀값으로 labelComponent(x, y)를 순환호출한다.
따라서 하나의 component를 만나는 경우 해당 component의 pixel은 전부 라벨링이 되는 것이다.