[자료구조] 자료구조와 알고리즘, 시간복잡도(Big-O 표기법)

728x90

Data(자료)란?

facts and statistics collected together for reference or analysis

참고 또는 분석을 위해 수집된 사실과 통계.

즉, 데이터는 현실 세계로부터 수집되는 사실(fact)이나 값(value) 또는 이들의 집합이며 가공되기 전의 상태를 뜻한다.

특정 목적을 위해 데이터를 가공하고 해석한 후의 상태를 우리는 정보(information)라고 한다.

자료구조(Data Structure)란?

자료구조란 데이터를 표현하거나 저장하는 방법이다.

효과적으로 설계된 자료구조는 프로그램 실행시간을 단축하고 메모리 용량을 최소한으로 사용하며 연산을 수행하도록 해준다.

따라서 프로그램을 설계할 때 가장 우선적으로 어떠한 종류의 자료구조를 선택해야 할지 고려해야 한다.

연산 방법과 목적 등에 따라 다양한 자료구조가 있으며, 일반적으로 아래와 같이 분류한다.

출처 : 그림으로 정리한 알고리즘과 자료구조 / 저자 조민호 / 정보문화사

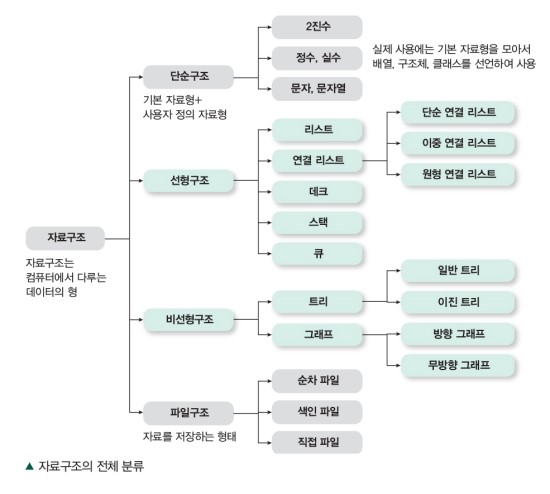
단순구조는 프로그래밍에서 사용되는 기본적인 자료형을 뜻한다.

선형구조의 자료구조는 데이터 간의 관계가 1:1로 형성되어 선형적으로 나열되는 구조를 가진다.

비선형구조는 데이터 간의 관계가 1:n 또는 n:m으로 형성되는 자료구조이다.

추상 자료형 (Abstract Data Type)

자료형이란 데이터와 연산의 집합을 뜻한다.

흔히 알고 있는 자료형인 int의 경우 4byte로 표현 가능한 정수 범위를 데이터로 가지며, 산술연산자(+, -, *, /, %)로 연산이 가능하다.

추상 자료형은 데이터 타입과 그 데이터와 관계된 연산들을 수학적으로만 정의한 것이다.

기능의 구현은 정의하지 않고, 데이터의 형태와 그 데이터의 연산만 추상적으로 정의를 한 상태인 것이다.

우리가 위에서 다룬 자료구조는 추상 자료형이 정의한 연산들을 구현한 구현체라고 보면 된다.

객체지향 프로그래밍에서의 클래스(Class) 개념과 유사하다.

Java를 예로 들자면 Class와 Interface의 차이를 생각해보면 된다.

알고리즘 (Algorithm)

위에서 언급했듯이 자료구조가 데이터를 표현하거나 저장하는 방법이라면, 알고리즘은 이렇게 저장된 데이터를 이용하여 문제를 해결하기 위한 절차나 방법을 의미한다.

좋은 알고리즘을 만들기 위해서 5가지의 조건이 있다.

입력 : 0개 이상의 입력이 존재하여야 한다.
출력 : 1개 이상의 출력이 존재하여야 한다.
명확성 : 각 명령어의 의미는 모호하지 않고 명확해야 한다.
유한성 : 한정된 수의 단계 후에는 반드시 종료되어야 한다.
유효성 : 각 명령어들은 실행 가능한 연산이어야 한다.

또한 알고리즘을 표현하는 방법에는 크게 4가지가 있다.

자연어
- 인간이 이해하기 쉬운 말로 설명되어 있는 형태이며, 단어들을 정확하게 정의하지 않으면 의미 전달이 모호해질 수 있다.
Flowchart (순서도)
- 직관적이며 이해하기 쉽지만, 복잡한 알고리즘의 경우 작성이 복잡해진다.
Pseudo-code (의사코드)
- 프로그래밍 코드를 흉내 내어 보다 간단하게 표현할 수 있는 코드이며, 알고리즘의 핵심 내용에만 집중할 수 있다.
Computer Language (프로그래밍 언어)
- 표현하고자 하는 대로 가장 정확하게 알고리즘을 기술할 수 있지만, 많은 코드로 인해 알고리즘의 핵심 내용의 이해를 방해할 수 있다.

시간 복잡도 & 공간 복잡도

효과적인 알고리즘을 얻기 위해 알고리즘의 성능을 분석하고 평가할 수 있어야 한다.

컴퓨터에서는 시간과 메모리 두 자원이 알고리즘의 효율성을 측정하는 척도가 된다.

알고리즘의 수행 시간을 분석한 결과를 시간 복잡도(time complexity)라고 하며, 메모리 사용량을 분석한 결과를 공간 복잡도(space complexity)라고 한다.

시간 복잡도는 알고리즘이 시작되어 완료되는 데까지 걸리는 시간을 의미한다.

하지만 실제 실행 시간은 하드웨어 성능 혹은 프로그래밍 언어에 따라 값이 달라지기 때문에 고려하지 않는다.

따라서 알고리즘에서의 시간 복잡도란 실행 명령어의 실행 횟수를 뜻한다.

공간 복잡도 또한 기본적으로 시간 복잡도와 동일하다. 다만 처리 시간 대신 메모리 사용량을 뜻한다.

시간복잡도 함수

알고리즘 수행에 필요한 전체 연산 수를 계산하면 실행 시간을 구할 수 있으며 이를 함수로 나타낼 수 있다.

예를 들어보자. (주석은 실행 빈도수를 뜻한다)

void f(int n){
  int cnt = 0;              // 1
  int sum = 0;              // 1
  for(int i=0; i<n; i++){
    cnt++;                  // n
    sum += i;               // n
  }
}

위의 알고리즘의 시간복잡도 함수는 $f(n) = 2n+2$이다.

n은 입력 개수를 뜻하며, n이 증가하면 그에 비례하여 시간도 증가한다.

Big-O 표기법 (Big-O Notation)

알고리즘의 시간복잡도와 공간복잡도를 표현하는 대표적인 방법에는 Big-O 표기법이 있다.

Big-O 표기법은 알고리즘 실행에 있어 최악의 경우를 나타낸다.

즉, 시간 또는 공간의 상한선을 두는 것이다.

Big-O 표기법 특징

만약 $3n²+10n+20$ 이라는 시간복잡도 함수가 있다.

입력값 n이 증가할수록 차수가 가장 큰 항이 결과값에 가장 큰 영향을 미치며, 다른 항들은 상대적으로 무시된다.

최고차항의 상수 계수 3 또한 가볍게 무시된다.

Big-O 표기법에서는 영향력이 없는 항과 상수 계수를 제거하고 실질적으로 가장 영향력이 큰 항(최고차항)으로만 시간 복잡도를 표현한다.

이렇게 원 함수를 단순화하여 최고차항의 차수만을 고려하는 표기법을 점근식 표기법(asymptotic notation)이라고도 한다.

Big-O 표기법의 수학적 정의

두 개의 함수 $f(n)$과 $g(n)$이 주어졌을 때, 모든 $n≥n₀$에 대하여 $|f(n)| ≤ c·|g(n)|$을 만족하는 2개의 상수 $c$와 $n₀$가 존재하면 $f(n)=O(g(n))$ 이다.

$f(n)$은 알고리즘의 시간복잡도를 의미하며 $g(n)$은 가장 영향력 있는 항을 뜻한다.

예를 들어보자.

$f(n) = 2n+1$ 이면 $O(n)$이다. (g(n) = n)
왜냐하면 n₀=2, c=3일 때, n≥2에 대하여 2n + 1 ≤ 3·n을 만족하기 때문이다.
$f(n) = 3n²+100$ 이면 $O(n²)$이다. (g(n) = n²)
왜냐하면 n₀=100, c=5일 때, n≥100에 대하여 3n² + 100 ≤ 5·n²을 만족하기 때문이다.

이해를 돕기 위해 그래프로 설명을 한다면 아래와 같다.

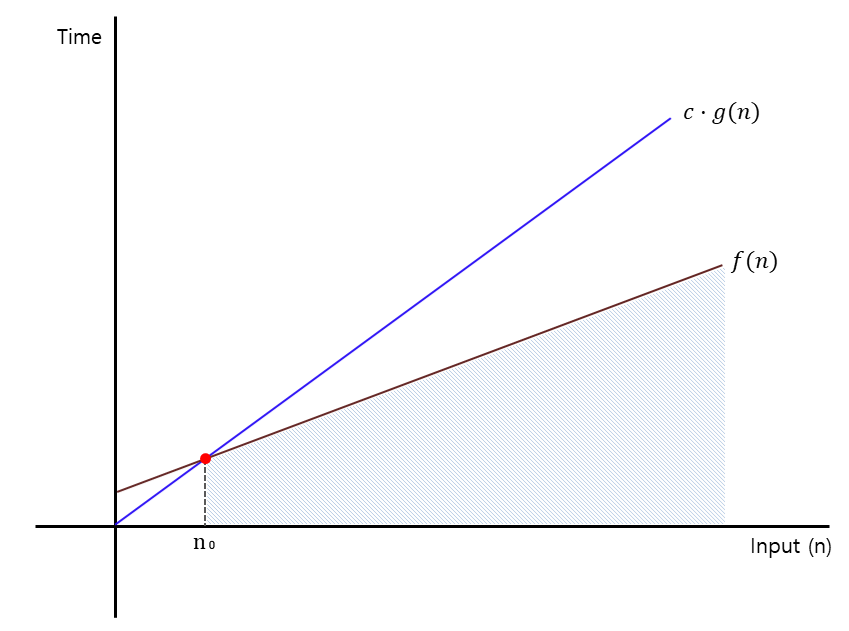
위에서 언급했듯이 $f(n)$은 알고리즘의 시간복잡도를 보여주는 그래프이며 최악의 경우를 나타낸다.

위 그래프에서 입력값 $n$이 $n_0$를 넘어갈 때부터 알고리즘 $f(n)$은 절대로 상한선 $c·g(n)$을 넘을 수 없음을 알 수 있다.

따라서 Big-O 표기법으로 알고리즘의 시간복잡도를 간단하게 표현할 수 있는 것이다.

Big-O 표기법의 종류 및 비교

$O(1) < O(log[n]) < O(n) < O(n*log[n]) < O(n²) < O(2ⁿ) < O(n!)$

오른쪽으로 갈 수록 비효율적이다.

이를 표로 나타내면 아래와 같다.

n값이 작을 때는 알고리즘 사이에 큰 차이가 없지만, n값이 무한대로 커질수록 알고리즘 수행 시간은 급격하게 차이가 난다.

※ 각 자료구조 연산 별 시간복잡도

Big-Ω & Big-θ 표기법

Big-O(Big-Omicron)는 시간 또는 공간의 상한을 나타내었다.

Big-Ω(Big-Omega)는 반대로 하한을 나타낸다.

Big-θ(Big-Theta)는 O와 Ω를 동시에 만족하는 경우를 의미한다.

즉, 어떤 알고리즘이 O(n)과 Ω(n)을 모두 만족해야만 θ(n)을 만족하는 것이다.

Big-O 표기법 사용

Big-Ω와 Big-θ 표기법이 있지만, 대부분의 경우 알고리즘의 시간복잡도를 표현할 때 Big-O 표기법만 사용한다.

여기서 중요한 사실이 있다.

예를들어 배열의 값을 찾는 알고리즘의 경우 시간복잡도를 O(n)으로 표현한다.

그러나 사실 Big-O는 함수의 상한만 표시하면 되므로 O(n²), 심지어 O(n!)로 표현해도 문제는 없다.

따라서 실제로는 Big-θ의 개념을 가지는 Big-O를 사용한다.

즉, 함수의 상한에 존재하는 시간복잡도 중 가장 작은 시간복잡도로 표현하는 것이다.

최선, 평균, 최악의 경우

일반적으로 알고리즘을 평가할 때 최선의 경우와 최악의 경우를 따지기도 한다.

평균은 계산하기가 까다로우므로 패스하자.

예를들어 배열 내의 어떠한 x값을 찾을 때 첫번째 index부터 순차적으로 찾는 알고리즘이 있다.

최선의 경우 첫번째 index에 x값이 위치하여 한번에 찾을 수 있을 것이다.

반면 최악의 경우 마지막 index에 x값이 위치하여 배열의 크기(n)만큼 전부 찾아야 할 것이다.

따라서 해당 알고리즘의 최선의 경우는 O(1), 최악의 경우는 O(n)이라고 말할 수 있다.

정리

Big-O, Big-Ω, Big-θ 모두 알고리즘의 정확한 성능을 계산하는 표기법이 아니다.

"데이터(n)이 많아 질수록 대충~ 이정도 성능이 나올 것이다"라고 대략적으로 평가하기 위한 것이다.

앞에서 설명했듯이 이를 점근식 표기법이라고 한다.