[Logic Gate] 4bit 가산기, 가감산기

이전 글

2020/06/29 - [IT/컴퓨터 시스템 개론] - [Logic Gate] 반가산기(Half-adder), 전가산기(Full-adder)

 

4-bit 가산기 (4-bit Ripple Carry Adder)

이전 글에서 전가산기의 경우 올림수(carry)를 포함하여 연산하기 때문에 n자릿수의 이진수 연산이 가능하다고 하였다.

이를 이용하여 4bit 이진수의 덧셈을 연산할 수 있는 4-bit 가산기를 만들어보자.

 

개요

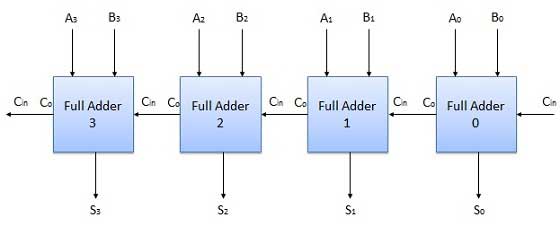
4개의 전가산기(FA, Full Adder)에 각각의 이진수 자릿수의 값과 이전 자릿수 연산에서 발생한 올림 값(Carry)이 입력되는 것을 볼 수 있다.

가장 오른쪽에 위치한 첫 번째 자릿수의 전가산기에는 0이 입력된다. (이전의 자리 올림수가 없기 때문)

 

논리회로

4-bit 가산기를 logic.ly에서 직접 그려보았다.

 

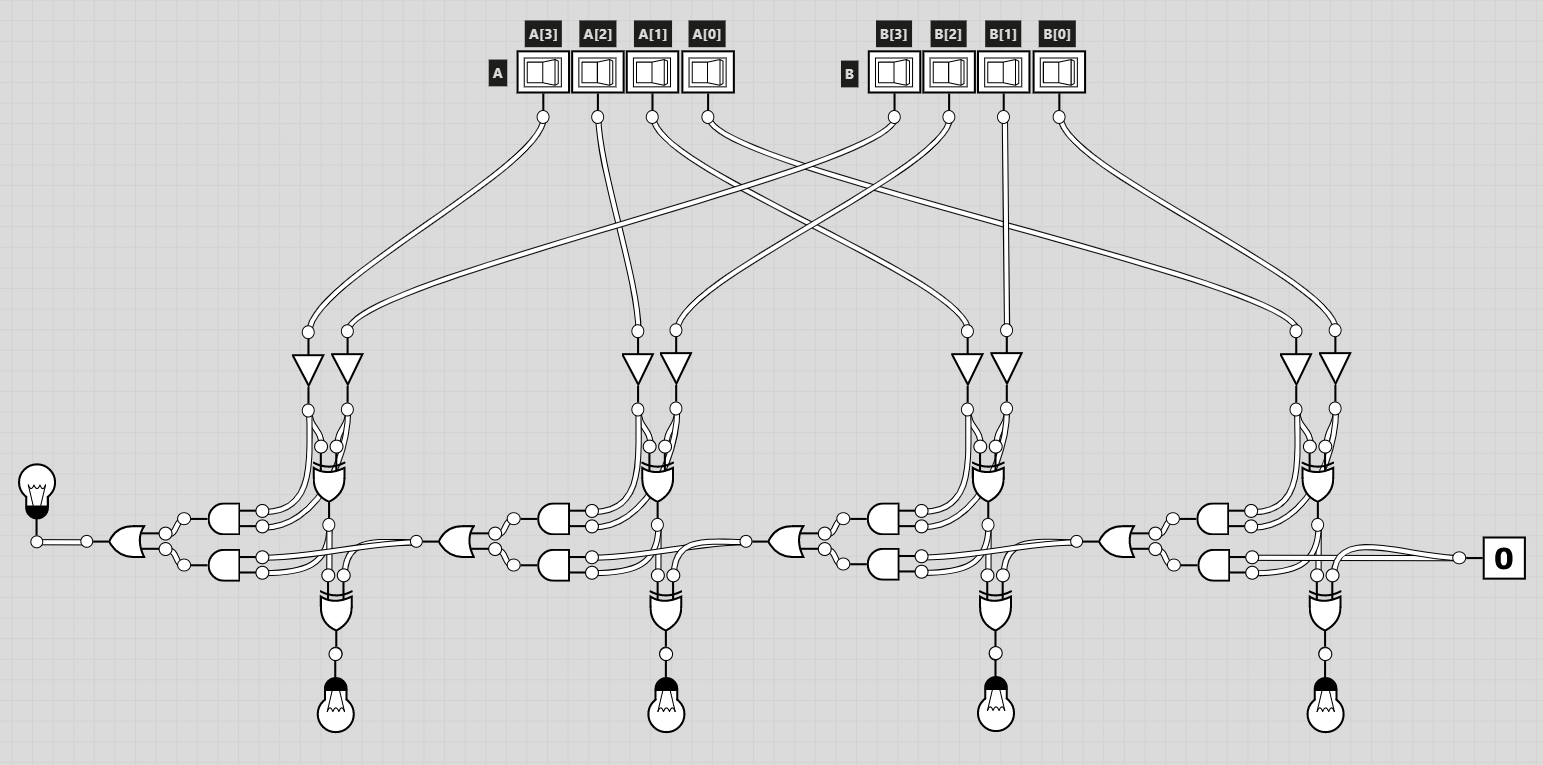
예제

1100⑵과 0011⑵을 더해보자.

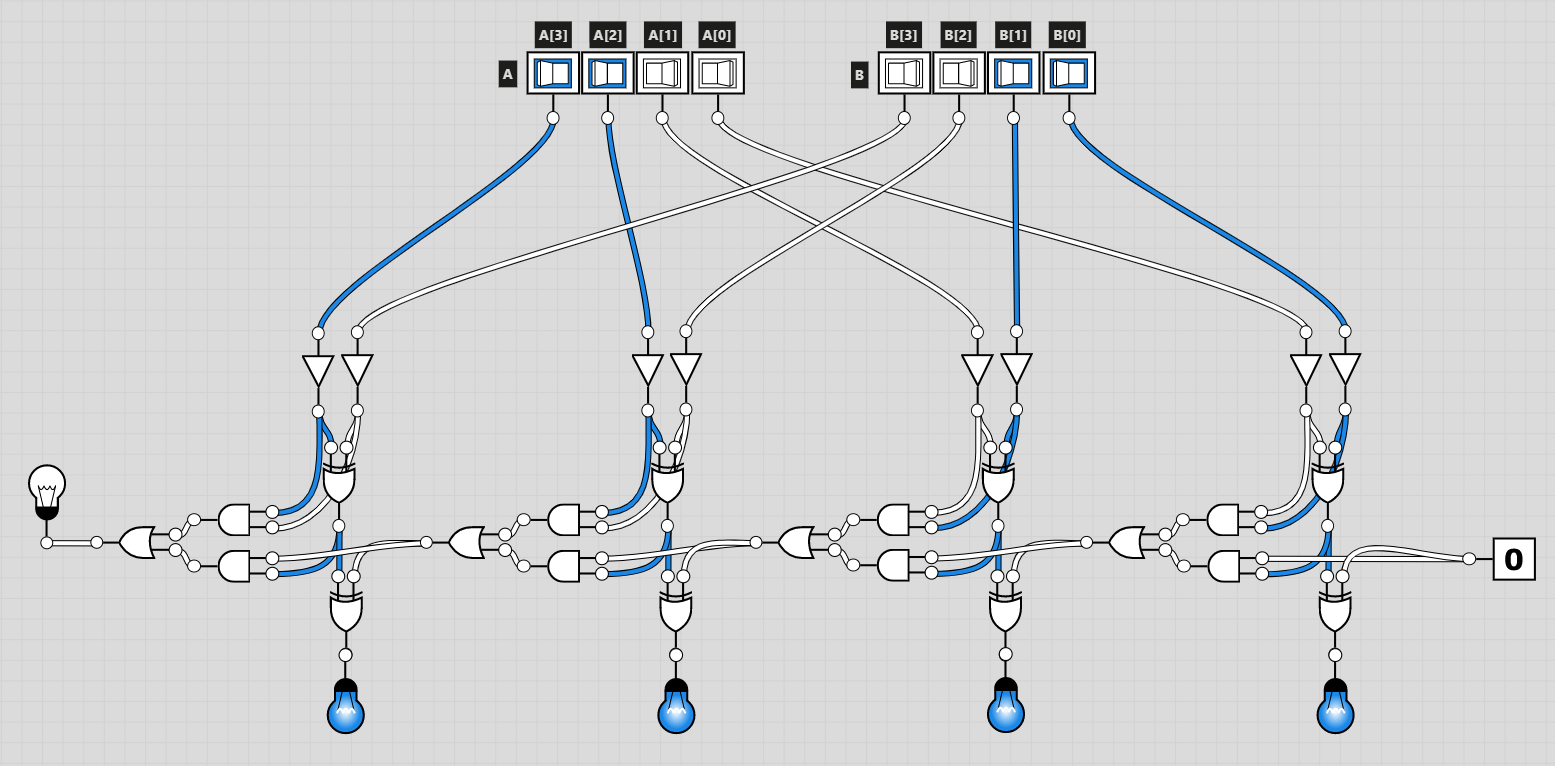
정상적으로 1111⑵이 출력되는 모습을 볼 수 있다.

 

만약 1100⑵과 0111⑵을 더하면 어떨까?

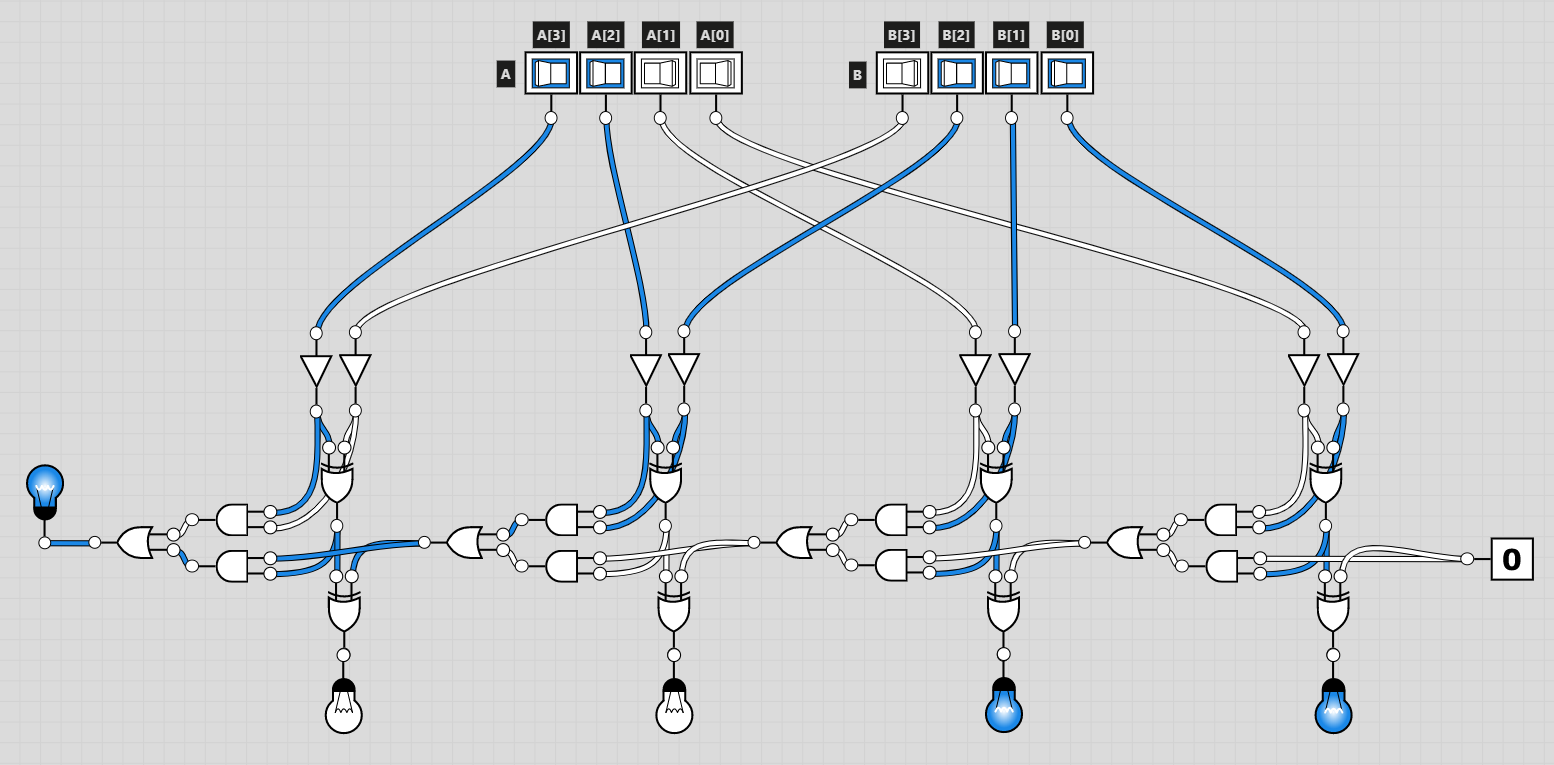
carry가 발생하고 정상적으로 출력되는 모습을 볼 수 있다.

10진수로 변환하여 검토를 해보아도 -4 + 7 = 3 임을 확인할 수 있다.

 

---

 

4-bit 가감산기 (4-bit Ripple Carry Adder/Subtractor)

지금까지 다룬 내용을 응용하여 4bit 이진수의 덧셈 뺄셈 연산이 모두 가능한 가감산기를 만들어보자.

 

개요

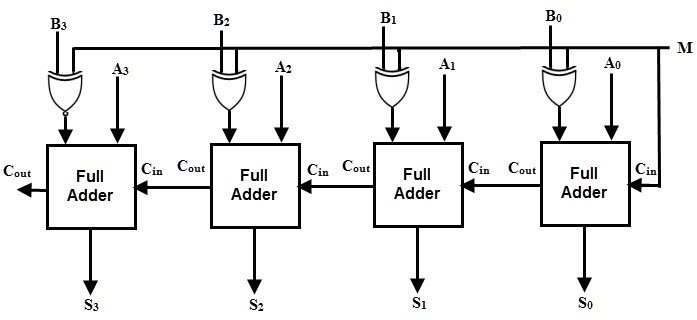
기존의 4-bit 가산기에 M(minus) bit값과 XOR연산이 추가된 것을 볼 수 있다.

이진수 A에서 B를 더하는 경우 M 값으로 0이 입력되고, A에서 B를 빼는 경우 M 값으로 1이 입력된다.

 

덧셈의 경우 M이 0이므로 0과 B의 XOR 연산을 거치면 B값이 그대로 빠져나온다.

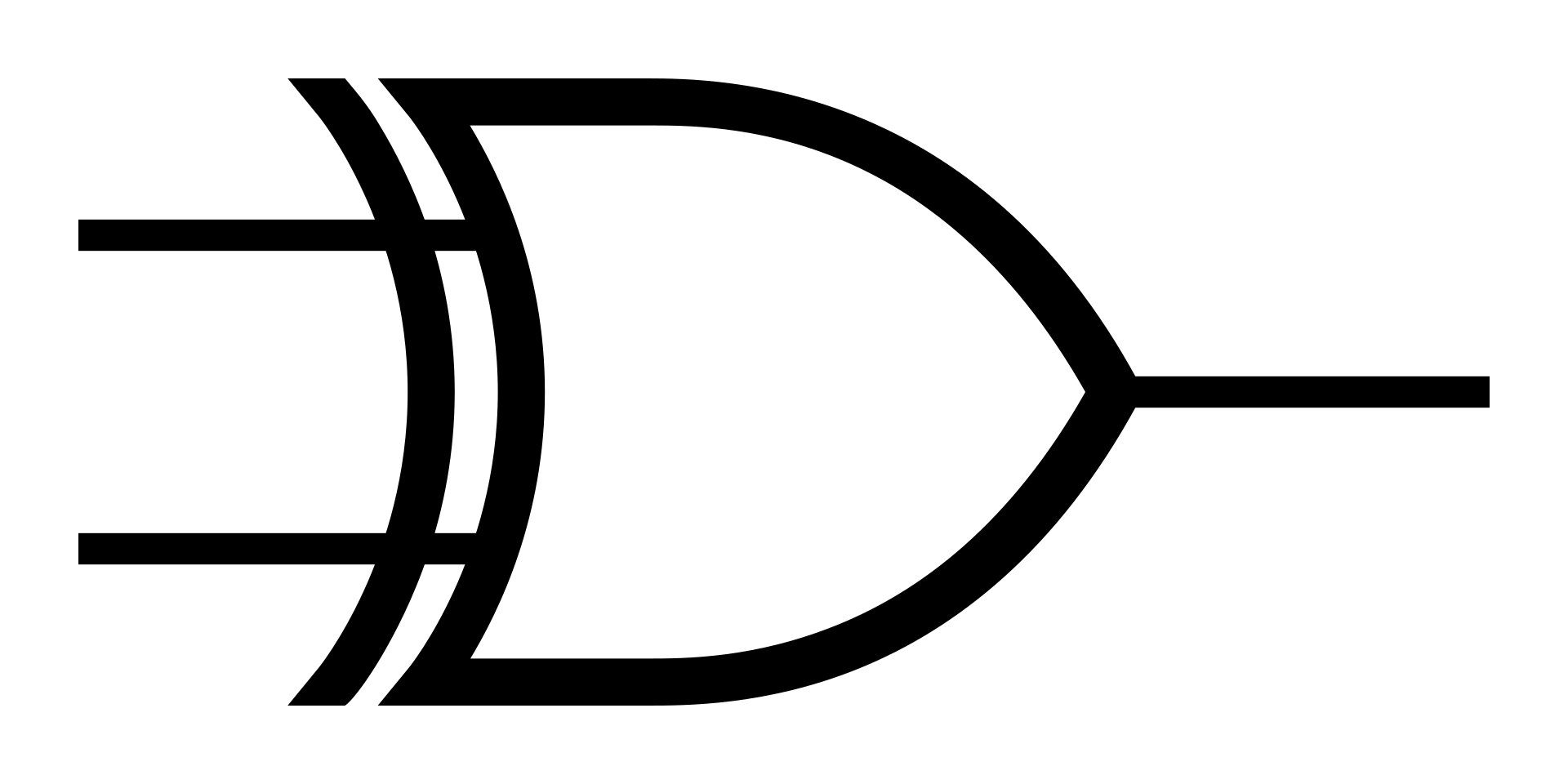
XOR(Exclusive OR) GATE

기호

진리표

Inputs		Outputs
B	M	B XOR M
0	0	0
0	1	1
1	0	1
1	1	0

따라서 온전한 A, B 값이 전가산기에 입력되고 이후로는 위에서 봤던 4-bit 가산기와 동일하게 연산이 수행된다.

 

뺄셈의 경우 A - B = A + (-B) 와 같다.

즉, B의 값을 음수로 바꾸면 우리가 위에서 다뤘던 4-bit 가산기를 이용해 쉽게 뺄셈 연산을 할 수 있다는 것이다.

 

B를 음수로 바꾸기 위해 B의 2의 보수를 구해야 한다.

(이진수의 음수 표현 방식에는 부호 절댓값, 1의 보수, 2의 보수 방식 등이 있으며, 일반적으로 컴퓨터에서는 2의 보수 방식을 사용한다.)

2의 보수를 구하는 방법은 이진수의 모든 자리의 숫자를 반전시킨 후 여기에 1을 더하면 된다.

 

M이 1이기 때문에 1과 B를 XOR 연산하면 B의 값이 반전되어 입력된다. (0이면 1, 1이면 0)

또한 첫 번째 자릿수의 전가산기에 Ci로 M값 즉 1이 입력되어 더해진다.

즉, B의 2의 보수를 구하여 전가산기에 입력하는 것이다.

따라서 A에 B의 음수 값을 더하는 방식으로 뺄셈을 진행할 수 있다.

 

논리회로

4-bit 가산기에 M과 XOR연산을 추가한 그림이다.

 

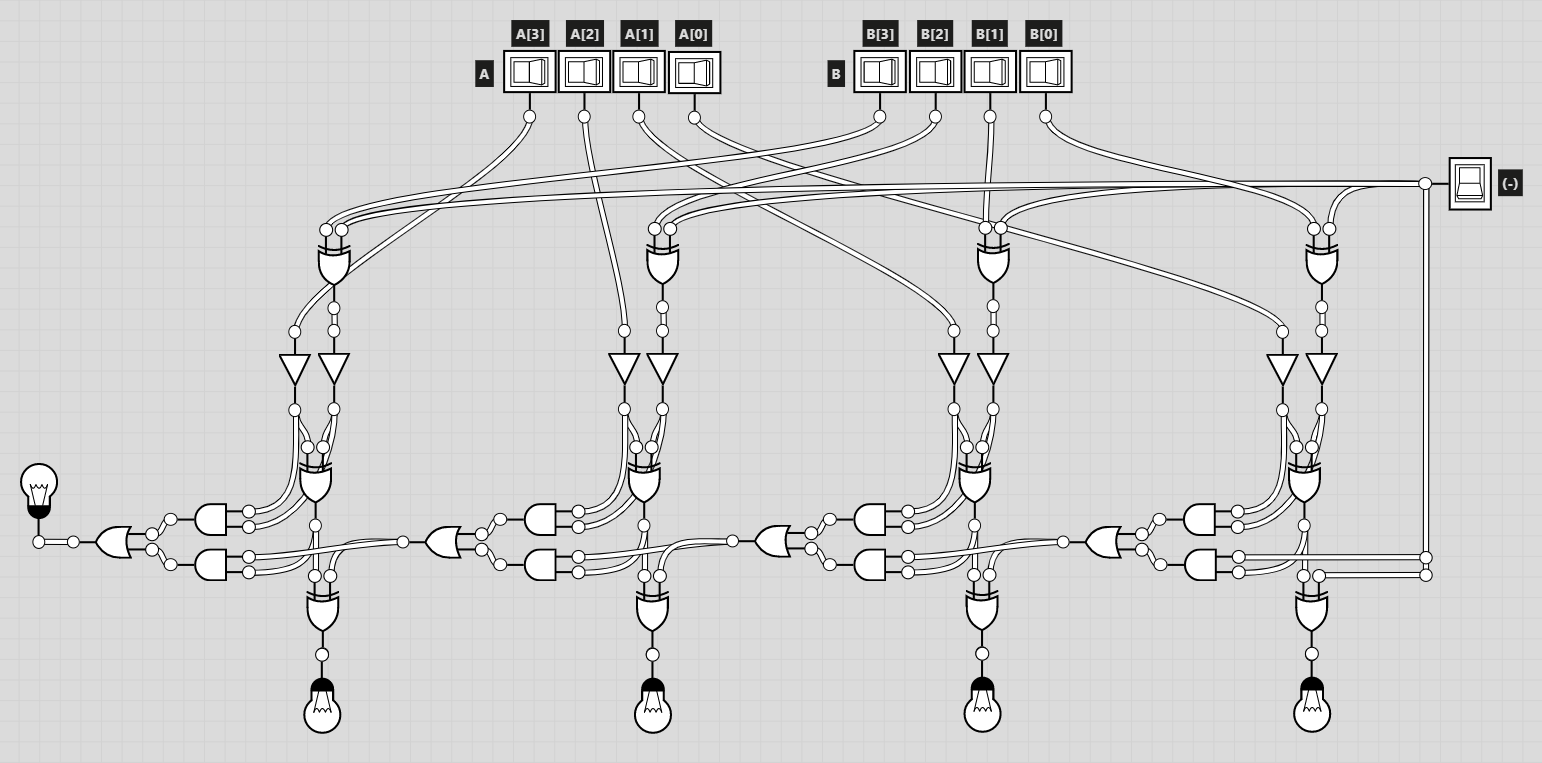
예제

7-2를 계산해보자.

A는 0111⑵이며, B는 0010⑵이다.

뺄셈 연산이기 때문에 Minus 버튼을 켜서 1을 입력한다.

정상적으로 5(0101⑵)가 출력됨을 확인할 수 있다.